General Description  Model Description  Simplifications  Glossary  Bibliography and Contributors

CMIS Educational Model

This simplified model predicts movement and degradation of pesticides in soils using soils, chemicals, daily rainfall and irrigation amounts, and daily evapotranspiration selected by the user. The software displays two soils side by side so comparisons can be made between different soils, chemicals, irrigation systems, and several other parameters. Soil and chemical properties along with cumulative infiltration amounts can be viewed on the output screen. The simplified model incorporates mass flow, dispersion, sorption, and degradation.

Art Hornsby and Ron Jessup at the University of Florida developed the split-screen technique as an educational tool. It was originally written in Basic and distributed on diskette with teaching materials for use in secondary schools.

Model Description

The simulation engine of CMIS may be divided into four module consisting of a transport module, a water flow module, a degradation module, and a distribution module. The transport module simulates chemical movement of the center of mass of the chemical due to water movement. The water flow module performs a water balance calculation in the soil using daily water inputs of rainfall and irrigation and water loss by evapotranspiration This module estimates the amount of water available to transport the chemical deeper into the soil profile.  The degradation module calculates the residual chemical mass in the profile. The distribution module estimates concentrations of the chemical at different locations in the profile using the depth of mass center from the transport module and the residual mass from the degradation module. The relative concentration is then displayed graphically by the software. The first three components of the model are contained in the CMLS model of Nofziger and Hornsby (1986).

I. Transport Module

Assuming that (1) chemicals move only in the liquid phase in response to soil-water movement, (2) all of the water in the soil is active in the flow process, (3) water already in the profile is pushed ahead of the inflowing water in a piston-like manner, (4) sorption can be described by the linear model, and (5) sorption is instantaneous and reversible, the depth of the chemical at time, t+dt, is given by (Nofziger and Hornsby, 1986)

where D_c(t) and D_c(t+dt) are the depths of chemical at time t and t+dt, respectively, q is the amount of water passing the depth D_c(t ) during time dt,  q_FC is the volumetric water content of the soil at “field capacity”, and R is the retardation factor of the chemical in the soil.  In this model, dt is taken as 1 day. The retardation factor is given by

where r is the bulk density of the soil and K_d is the partition coefficient of the chemical in the soil. For many soils and organic chemicals, K_d can be estimated from organic carbon content of the soil and organic carbon partition coefficient of the chemical (Hamaker and Thompson, 1972 ; Karickhoff 1981, 1984) using the equation

where OC is the organic carbon content of the soil and K_oc is the organic carbon partition coefficient of the chemical.  The organic carbon content of the soil is assumed to be uniform with depth in this simplified model.

Figure 1. Conceptual diagram of soil-chemical system

II. Water Flow Module

The water module calculates a daily water balance in the root zone to determine the amount of water, q, available to move the chemical deeper into the soil (see Figure 1). In this model, water can be removed from the root zone by evapotranspiration and by drainage into the soil below the root zone. Water enters the soil at the soil surface as rainfall and irrigation. Each day the program reduces the water in the root zone for evapotranspiration on that day. It then adds water to the soil equal to the amount of rainfall and irrigation on that day. If the soil above the chemical is capable of storing all of the infiltrating water, no water is available for leaching the chemical deeper into the soil. If more water enters the soil surface than can be stored above the chemical, this excess water will tend to move the chemical downward. The program updates the water content of the soil above the depth of the chemical and in the remainder of the root zone each day so that this calculation can be carried out. The following paragraphs summarize these steps in mathematical terms.

For purposes of calculating q, it is convenient to consider the soil to be composed of 3 layers (See Figure 1). One layer has a bottom at the depth of the chemical (that is, D_c(t)), one layer ends at the bottom of the root zone, and one layer extends to some large depth below the root zone. Initially the depth of chemical is above the root zone depth. As time passes that boundary moves downward so that at large times it may exceed the root depth.

The amount of water passing the chemical at depth D_c(t) during time dt is determined from water balance calculations of all the element layers during the time interval dt (taken as 1 day in the model).  The water balance analysis is done layer by layer progressively starting from the surface layer.  The amount of water passing the bottom of layer j during an interval from t to t+dt may be expressed as

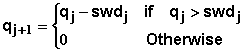
where q_j and q_j+1 are the amount of water passing the bottoms of the (j-1)th and jth layer, q₀ is the total infiltration occurring during time dt, and swd_j is the soil water deficit of layer j at time t or the amount of water required to recharge layer j to field capacity. The soil water deficit of layer is given by

where T_j the thickness of layer j, q_FC is the volumetric water content of the layer at field capacity, q_j(t) is the volumetric water content of layer j at time t, and ET_j(t) is the evapotranspiration loss from layer j during the interval from t to t+dt. ET_j(t) is estimated using the equation

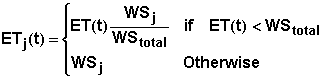
where ET(t) is the total evapotranspiration loss from the root zone during the interval from t to t+dt; WS_j the available water stored in layer j at time t, and WS_total is the amount of water stored in the root zone at time t.  The available water stored in layer j at time t is given by

where q_PWP is the water content of the layer at permanent wilting point. In the root zone, the water content of layer j at time t+dt may be express as

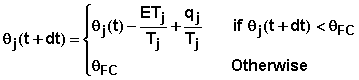
where  q_j(t+dt) is the water content of layer j at time t+dt.  For layers below the root zone, the water content is equal to the field capacity at all times.  Thus water passing the root zone depth passes all depths below that.

III. Degradation Module

Degradation of the chemical in the soil is simulated by first-order kinetics.  The amount of chemical per unit surface area remaining in the soil at time t+dt is given by

where M(t) and M(t+dt) represent the amount of chemical at times t and t+dt, respectively and H is the degradation half-life of the chemical.

IV. Distribution Module

The transport and degradation modules of the program predict depth of the center mass and the amount of a chemical remaining at different times.  The following equation is employed to approximate the concentration distribution of the chemical in the soil profile (DeSmedt and Wierenga, 1978; Dayananda et al., 1980; Rose et al., 1982a, 1982b, 1982c).

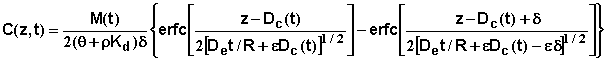
where C(z,t) is chemical concentration at depth z and time t, d is an initial width of chemical pulse (e. g. the depth of incorporation), e is a dispersivity factor, D_e is the molecular diffusion coefficient, and erfc is the complimentary error function.

Assumptions and Simplifications

This simplified model contains the following assumptions and simplifications.

Transport Module:

1. Chemicals move only in the liquid phase.
2. Dispersion of the chemical can be ignored.
3. Soil and chemical properties are uniform within a soil layer.
4. All water in the profile takes part in the flow process. Water already in the soil profile is pushed ahead of infiltrating water in a piston-like manner.
5. The sorption process can be described by the linear, reversible, equilibrium model.
6. The chemical does not move upward anywhere in the profile.

Water Flow Module

1. Infiltrating water recharges one layer of soil to field capacity before moving deeper into the soil.
2. Infiltrating water redistributes instantly to field capacity.
3. Water content of soil below the root zone is never less than field capacity.
4. The amount of water removed by evapotranspiration from each layer of the root zone is proportional to the amount of available water in that layer.
5. The water content of the soil does not decrease below the permanent wilting point.
6. Water does not move upward from below the root zone.

Degradation Module

1. The degradation process is a first-order process.
2. The degradation rate in each layer in not a function of time or position.

Distribution Module

1. The distribution equation is merely an approximate one imposed onto the transport and degradation modules.
2. This approximate distribution equation was obtained by modifying another approximate solution proposed by De Smedt and Wierenga (1978), Dayananda et al. (1980), and Rose et al. (1982a, 1982b, 1982c).
3. The approximate distribution equation simulates the advancing and spreading of a chemical pulse with an initial width of d.
4. For purposes of this software, d is taken as 10 cm, D_e is taken as 0.2 cm² day^-1, and  e is taken as 0.50 cm.

Glossary

Dispersivity: Dispersivity is the ratio of dispersion coefficient to pore-water velocity. It is on the order about 1 cm or less for disturbed (repacked) soils and for certain uniform field soils. For transport problems involving undisturbed field soils, especially when aggregated, the value of dispersivity is usually about one or two orders of magnitude larger than that of repacked soils (van Genuchten and Wierenga, 1986).

Field Capacity: Field capacity is usually defined as the amount of water remaining in a soil system after downward gravity drainage has ceased, or materially done so, after a period of rain or excessive irrigation to thoroughly wet the soil system(Bear, 1972; Marshall and Holmes, 1988).

First-order kinetics: First-order kinetics refers to a reaction process of which the reaction rate is proportional to a concentration of the component in the system. The proportionality constant is called the first-order rate constant. In a degradation reaction, the first-order rate constant is also referred to as the first-order decay constant.

Partition Coefficient: Partition coefficient is the ratio of the content of a chemical species in the adsorbed phase to the concentration of that chemical species in the liquid phase.

Organic Carbon Partition Coefficient: Organic carbon partition coefficient is the ratio of the partition coefficient of a chemical species in a soil to the organic carbon content of the soil.

Permanent Wilting Point: Permanent wilting point is defined as the water content of a soil when indicator plants growing in that soil wilt and fail to recover when placed in a humid chamber (SSSA, 1984).

Bibliography

Bear, J., 1972. Dynamics of fluids in porous media. Dover Publications, Inc., 31 East 2^nd Street, Mineola, NY 11501, pp. 483-484.

Dayananda, P. W. A., F. P. W. Winteringham, C. W. Rose, and J. Y. Parlange. 1980. Leaching of a sorbed solute: a model for peak concentration displacement. Irri. Sci., 1:169-.

De Smedt, F. and P. J. Wierenga. 1978. Approximate analytical solution for solute flow during infiltration and redistribution. Soil Sci. Soc. Am. J., 42:407-412.

Hamaker, J. W and J. M. Thompson. 1972. Adsorption. In C. A. I., and J. W. Hamaker (ed.) Organic chemicals in the environment. Marcel Dekker Inc., NY. pp 49-143.

Hillel, D. 1998. Environmental Soil Physics. Academic Press, Inc. 525 B Street, Suit 1900, San Diego, CA 92101-4495.

Karickhoff, S. W. 1981. Semi-empirical estimation of sorption of hydrophobic pollutants on natural sediments and soils. Chemosphere 10:833-846.

Karickhoff, S. W. 1984. Organic pollutant sorption in aquatic systems. J. Hydr. Eng. 110:707-735.

Marshall, T. J. and J. W. Holmes. 1988. Soil Physics. 2nd edition. Cambridge University Press. 32 East 57th Street, New York, NY 10022.

Nofziger, D. L. and A. G. Hornsby. 1986. A microcomputer-based management tool for chemical movement in soil. Applied Agric. Research 1:50-57.

Rose, C. W., F. W. Chichester, J. R. Williams, and J. T. Ritchie. 1982a. A contribution to simplified models of field solute transport. J. Environ. Qual., 11:146-150.

Rose, C. W., F. W. Chichester, J. R. Williams, and J. T. Ritchie. 1982b. Application of an approximate analytical method of computing solute profiles with dispersion in soils. J. Environ. Qual., 11:151-.

Rose, C. W., W. L. Hogarth, and P. W. A. Dayananda. 1982c. Movement of peak solute concentration position by leaching in a nonsorbing soil. Aust. J. Soil Res., 20:23-.

SSSA. 1984. Glossary of soil science terms. Soil Science Society of America, Madison, WI.

van Genuchten M. T. and P. J. Wierenga. 1986. Solute dispersion coefficients and retardation factors. In A. Klute (ed.) Methods of soil analysis. Part 1 Physical and mineralogical methods. Second edition. SSSA, Madison, WI.

Contributors

This program was designed by Dr. D. L. Nofziger and J.Wu,  Department of Plant and Soil Sciences, Oklahoma State University, Stillwater, OK 74078.

Send email to david.nofziger@okstate.edu

Last Modified: January 16, 2008